突然ですがあなたに好きな定理はありますか?

少し考えてみてください。
答えは
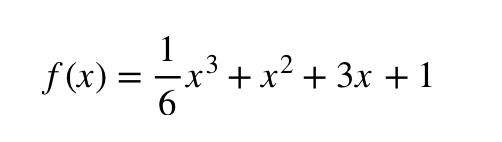
となります。どうでしたか?恐らくこれくらいは解けたかと思われます。では次の問題です。

これも少し考えてみてください。
答えが
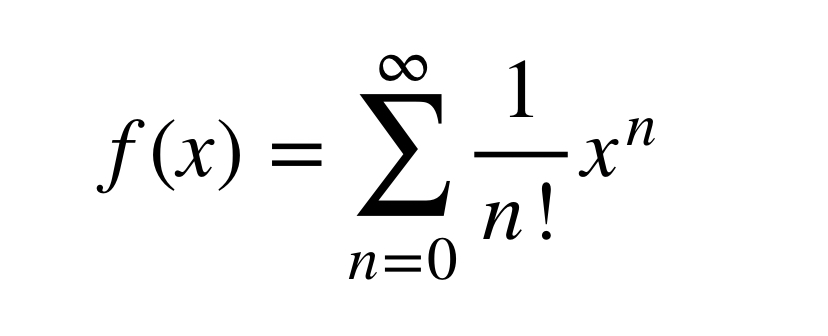
になりましたか?
それとも
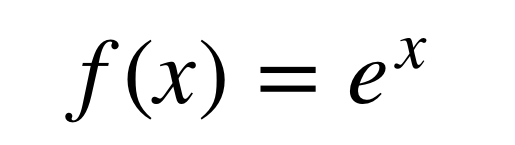
になりましたか?
どちらも条件を満たします。一体どういうことでしょうか?答えが2つあったってだけな気もしますが実は
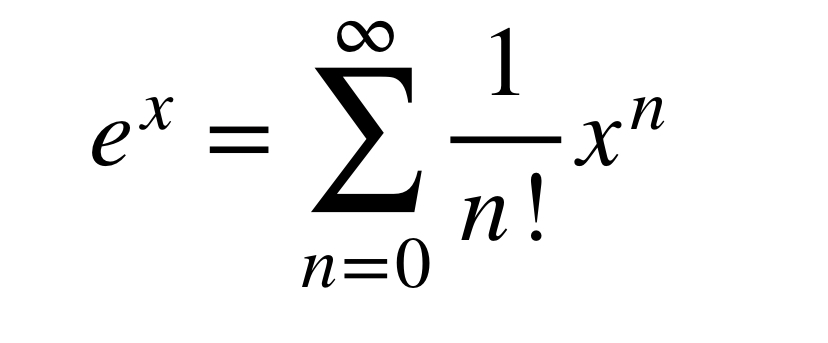

項を片方に寄せて関数とみなして微分して増減を調べて解くのが受験数学の定石でしょうが、こういう形の不等式問題*5が寄せて微分で確実に解けるのにはちゃんと数学的背景があったんですね。
今までの議論から以下の式の意味がなんとなく分かると思います。*6
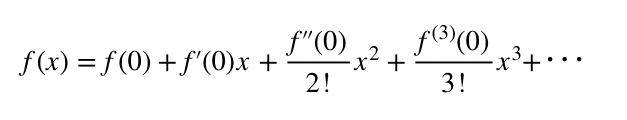 このような関数の展開方法をマクローリン展開と言います。マクローリン展開した式を途中でちょんぎったものは0近傍についてのf(x)の近似になっています。下のグラフを見てみて下さい
このような関数の展開方法をマクローリン展開と言います。マクローリン展開した式を途中でちょんぎったものは0近傍についてのf(x)の近似になっています。下のグラフを見てみて下さい
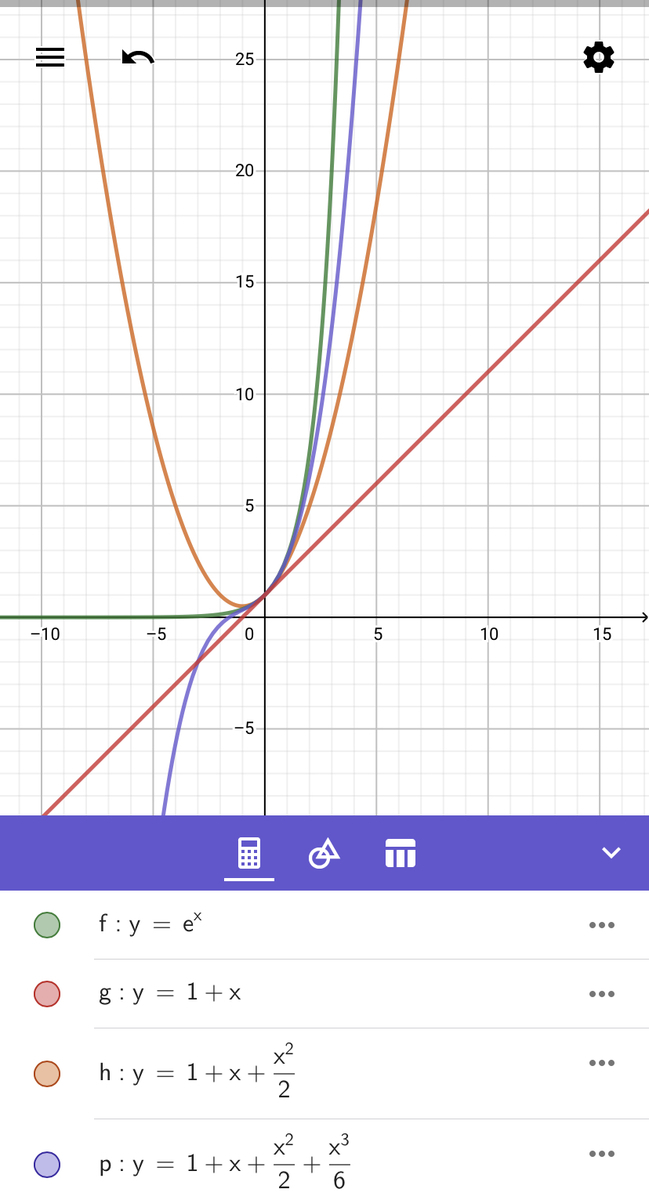
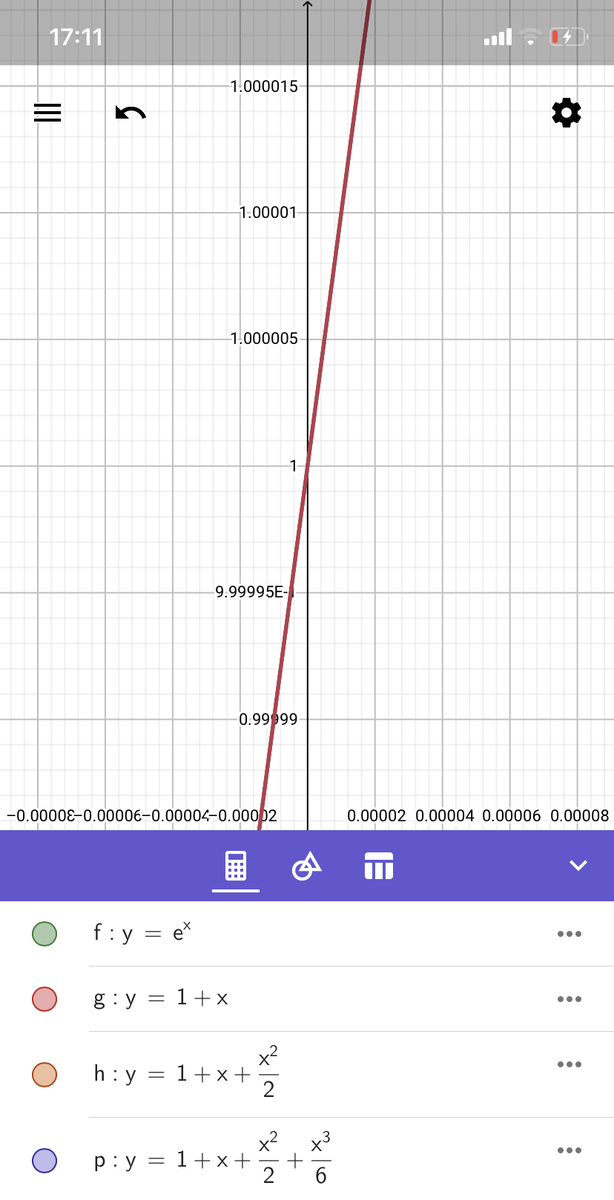
分かりますかね?より高次の項までとってきた方が元の関数に近づくということと、0付近ではよく近似出来ているということの2つの事柄をグラフで表現しているのです。より一般に0だけではなく関数の定義域内の定数aに対しては
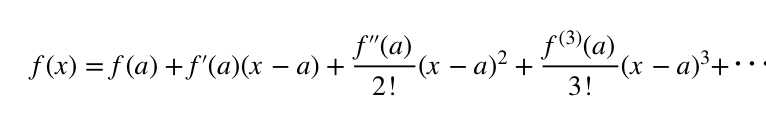
となります。これをテイラー展開*7といいます。要するにテイラー展開というのは途中でちょんぎったりして関数を多項式で近似するためのものなんですね。
ではここでsinxとcosxをマクローリン展開してみて下さい。本来マクローリン展開可能かなどを考慮しなければいけませんがsinxとcosxは任意の実数*8でマクローリン展開可能として下さい。
出来ましたか?
答えはこうなります。
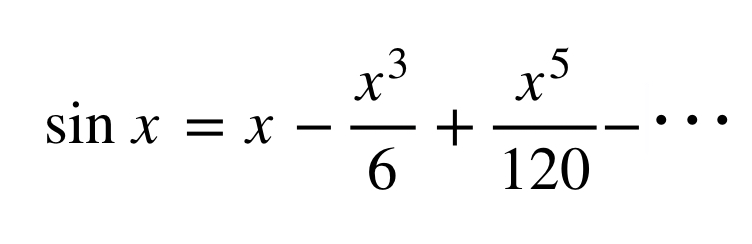
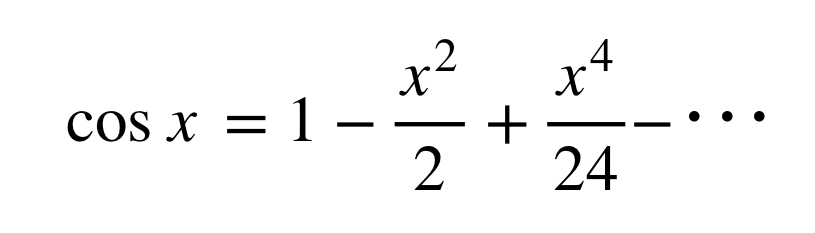
途中でちょんぎったものが0付近での近似に相当することを踏まえたら数Ⅲで習う極限の諸公式がより馴染みの深いものになると思います。途中でちょんぎったもののグラフを書いてみるとより理解が進むと思います。
さてここでe^xのマクローリン展開の式にiθ(θは任意の実数)を代入すると
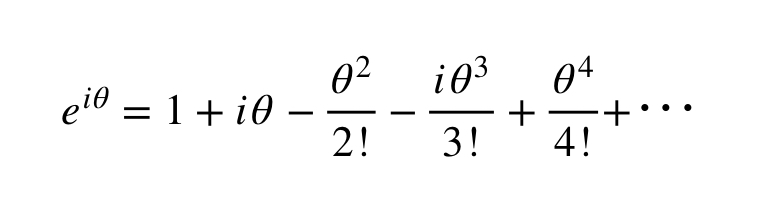
となりますよね?上の三角関数のマクローリン展開の式とこの式をよ〜く見比べて下さい。何か気づきませんか?
なんと以下の式が成立するのです!!
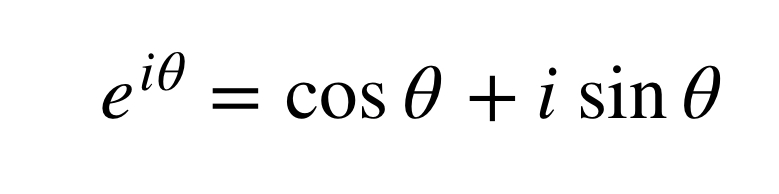
工学ではこの式をよく使います。なので工学系の人にオイラーの公式というとこれを連想されるそうです。上の式を使うと三角関数の様々な公式、例えば加法定理などを容易に証明することが出来ます。
あとは上の式にθ=πを代入し-1を移項すると…
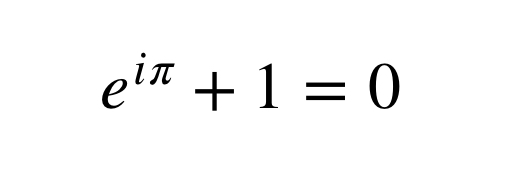
ついに世界一美しい式とも評されるオイラーの公式が示されました!
どうでしたか?細かい議論はしていませんがテイラー展開の雰囲気とオイラーの公式の証明の大筋は理解して頂けたと思います。
疑問点があればDM下さい!
ではまたの機会に!